Tutorial - Bitwise Operations

Get wise with bitwise!

If you have any sort of computer science background, the term bitwise should come second-nature to you. If you're not, then here's a quick rundown.

Bitwise Basics

Computer programs don't store numbers as the numbers we know in base-10, they store them as bytes. What's a byte? A byte is a bunch of 1s and 0s bunched together. The single element (the 1 or 0) is just called a bit. The computer program looks at the bits in the byte and reconstructs the number we're looking for by using each bit's place value as a power of two.

Huh?!

In our traditional base-10 math, if we have the number 152, we could break it up into 100 + 50 + 2. We could then express each of those numbers as a number times a power of ten. So 152 = 100 + 50 + 2 = (1 x 10^2) + (5 x 10^1) + (2 x 10^0). To express that we can just go 1 5 2. Which is stupidly obvious.

What if we're restricted to base 2 (aka binary, just a 1 or 0, like computers) and have the number 12? Powers of 2 are 1, 2, 4, 8, 16, 32, 64 … etc etc. So to get 12 out of that we could just go 8 + 4. So our base 2 number would look like (1x2^3) + (1x2^2) + (0x2^1) + (0x2^0). Or just 1 1 0 0. That 12 is actually being store as 1100 inside the computer program.

Using in FRED

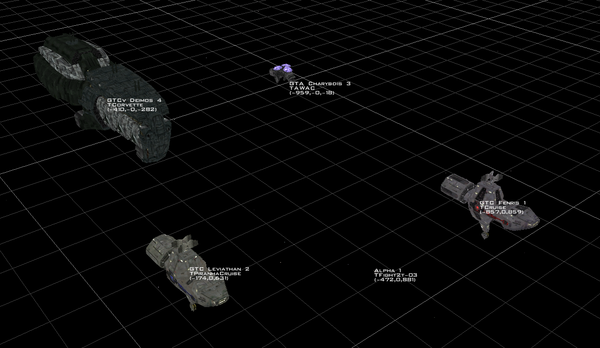
Imagine we have a campaign going with 4 persistent ships.

Our wonderful fleet.

How could we easily keep track if they are alive or dead? (Let's pretend that the health of each ship doesn't matter, just if they're alive or dead.) is-previous-event-false ShipAWasDestroyed? Sure, but if our campaign is going to be long, you're going to be checking a lot of previous events. Put its status in a variable? This is good, but updating 4 variables throughout a campaign? What a… pain.

Hey, look at that bitwise example above. If our variable's bits corresponded to the status of our ships, that could work. So 1 1 1 1 would be all four ships are alive. 1 0 1 0 would be 2 ships alive, 2 dead, 0 1 0 1 would be the other 2 ships alive and the other 2 dead. Let's see how we could accomplish this.

When we make a new integer variable in FRED, a common default value is 0, but inside FRED there's quite a few more zeroes. An integer variable inside FRED is 4 bytes, or 32 bits. This means FRED really is storing 0000 0000 0000 0000 0000 0000 0000 0000 for the default value of 0 (spaces added to help with readability). So we could theoretically store 32 ships with this system, but we'll just stick to 4 for the time being.

So when we store our ship's status, we want 1 1 1 1 since they are all alive. We would NOT just type in 1111, because in binary that is actually 0100 0101 0111. Not quite what we're looking for. Constructing the number in binary and be tricky for people unfamiliar with binary (FYI its 15). So maybe instead of making each bit "is this ship alive?" we could just think of each bit as "is this ship dead?" That way we can just keep our initial value at zero.

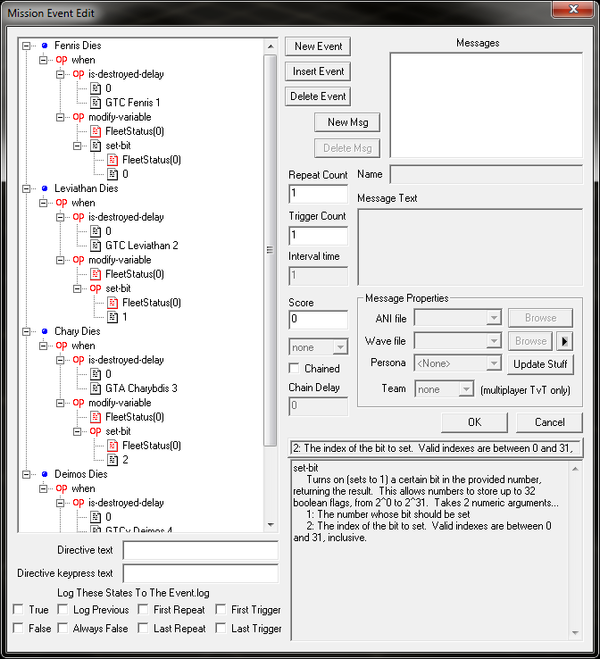
Now how do we modify our variable properly if a ship dies? This nifty set-bit sexp. Now the set-bit operator only returns the value of a variable after a specific bit is set. Set-bit by itself doesn't modify the variable, we still need to use the modify-variable sexp first. But it's still simple enough to use.

"Modify FleetStatus to be FleetStatus with Bit Index 0, 1, 2 or 3 set" (Quick note, computers love to start counting at 0, so index 0 is technically the first bit)

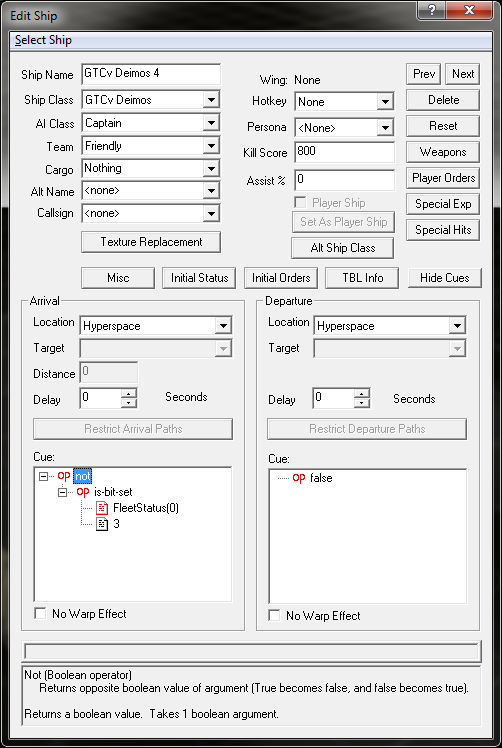
Then at the beginning of each mission (or the arrival cue) we just check a bit's status with is-bit-set to see if it should arrive.

Yes, using bit-wise operations with integer variables allows you to cram 32 true/false variables into that single variable.

To get into some real advanced things, you can also play with bitwise AND, OR and XOR operators. Check out this wikipedia article for more great info on those.

If you need more than true or false, you could do similar things with string-get/set-substring. It works similar to the bitwise operators, it only affects a desired section of the variable. For instance you could store things like morale levels for a squad of fighters, a rough health status for turrets, or responses when a player was asked a question. Things can get pretty complicated though, so take things nice and slow.